Friday, October 30, 2015
Sunday, October 25, 2015
Long and Synthetic Division
Hi there! Let's review the first part that we've covered in Unit 3 so far. In this unit, we mostly use division to find the answers, which could be either Long Division or Synthetic Division. However, there are certain points that we have to remember when use these methods.
Example 1: Divide 16t + 6t³ - 4- 19x² by t -2
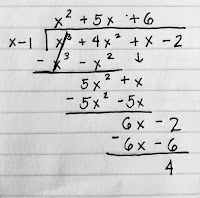
OR WE CAN USE,
x³ +4x² +x -2 ÷ x -1 = x² +5x +6
Factor the quotient x² +5x +6
A remainder of more than 0 means the divisor is not a factor of the given polynomial
To conclude, it's way easier to use synthetic division but try doing long division once in a while since it's a good practice.
Example 1: Divide 16t + 6t³ - 4- 19x² by t -2
-Always
arrange the terms from
highest
to lowest degree
-Use subtraction
OR WE CAN USE,
-The arrangement of the coefficients is based from
highest to lowest degree
-Use Addition
-The divisor will be 2 because (x-a) → t-2 → x=2
- 6t³ -19t² +16t -4 ÷ t -2 = 6t² -7t +2
- Factor the quotient 6t² -7t +2
6t² -4t -3t +2
2t (3t-2) -1 (3t -2)
(2t -1) (3t-2)
Answer: 6t³ -19t² +16t -4 = (2t -1) (3t-2) (t -2)
A remainder
of 0 means the divisor is a factor of the given polynomial
Example 2: Divide x
-2 +4x² +x³ by x -1
Long Division
-Arrange
the terms from
highest
to lowest degree again
-Use
subtraction
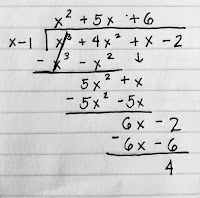
Synthetic Division
-The arrangement of the coefficients is based from
highest to lowest
-Use Addition
x² +5x +6
x² +3x +2x +6
x(x+3) 2(x+3)
(x+2) (x+3)
A remainder of more than 0 means the divisor is not a factor of the given polynomial
To conclude, it's way easier to use synthetic division but try doing long division once in a while since it's a good practice.
Tuesday, October 13, 2015
Going Backwards with Transformations
A couple
of days ago, we learned how to graph y= f(x) if the transformed function is
given. We can determine the original function y=f(x) when the transformed
function is given, by first determining what transformation(s) occurred in the
function. Then, reverses the steps of transformation(s) after doing so, apply the
opposite operation to the x and y point(s).
Example:
-
Given
the transformed function y= 2f ½ (x+2) -1 below. What is the graph of y= f(x).
Transformation: To get y= f(x)
- Multiply y-values by 2 - Add 1 from y-values
-
Subtract 1 from y-values - Divide y-values by 2
-
Multiply x-values by 2 -
Add 2 from x-values
-
Subtract 2 from x-values - Divide x-values by 2
y= 2f ½ (x+2) -1 y= f(x)
(-1,
1) (½,
3/2)
(2, -2) (5/2, -½)
(4,-2) (4, -½)
(6, 0) (5, ½)
Tuesday, October 6, 2015
Subscribe to:
Comments (Atom)











