Long and Synthetic Division

Hi there! Let's review the first part that we've covered in Unit 3 so far. In this unit, we mostly use division to find the answers, which could be either Long Division or Synthetic Division. However, there are certain points that we have to remember when use these methods.


Example 1: Divide 16t + 6t³ - 4- 19x²  by t -2

Long division                                                                     

-Always arrange the terms from                                      

highest to lowest degree

-Use subtraction                                                               

                                                                                             

OR WE CAN USE,

Synthetic Division

 -The arrangement of the coefficients is based from

 highest to lowest degree

 -Use Addition

-The divisor will be 2 because (x-a) → t-2 → x=2

• 6t³ -19t² +16t -4 ÷  t -2 =  6t² -7t +2
• Factor the quotient 6t² -7t +2 

       6t² -7t +2                                                            

       6t² -4t -3t +2

       2t (3t-2) -1 (3t -2)

       (2t -1) (3t-2)

Answer:  6t³ -19t² +16t -4 =  (2t -1) (3t-2) (t -2)

A remainder of 0 means the divisor is a factor of the given polynomial

Example 2: Divide x -2 +4x² +x³ by x -1

Long Division                                                                                        

-Arrange the terms from                                                                    

highest to lowest degree again                                                         

-Use subtraction

OR WE CAN USE,

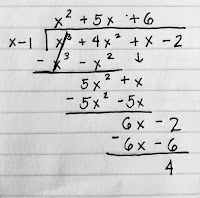
 Synthetic Division

 -The arrangement of the coefficients is based from

 highest to lowest

  -Use Addition

-The divisor will be -3 because (x-a) → t+3 → x= -3

x³ +4x² +x -2 ÷  x -1 =  x² +5x +6

Factor the quotient x² +5x +6

x² +5x +6

x² +3x +2x +6

x(x+3) 2(x+3)

(x+2) (x+3)

A remainder of more than 0 means the divisor is not a factor of the given polynomial

To conclude, it's way easier to use synthetic division but try doing long division once in a while since it's a good practice.