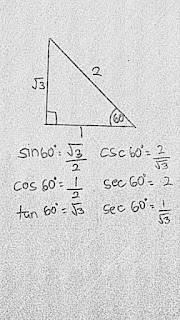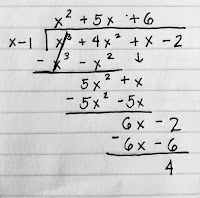Proving Trigonometric Identities

Hi friends! Yesterday we finished up the lesson on Proving Trig Identities. I'm going to give quick a run through on how to prove identities. ♪~ ᕕ(ᐛ)ᕗ

To prove an identity:

• Simplify each expression on either side of the equal sign in your equation given, so that both sides are equal. This means that the expression on the left hand side is equal to the expression on the right hand side. Not to be mistaken for verifying an identity, where you substitute values that make the statement true.

 Let's start simple, given the example 

sin²x + cos²x  = 1
↑
left hand side

Looking at the left hand side, we know that sin²x + cos²x is also equal to 1. This can then be simplified to 1, since they both represent the same thing. The equation then turns into:

1 = 1

When you make sure both sides of the equation are simplified, you make sure that they are both equal to eachother. In this case both sides need to equal 1, which is correctly stated above.

This equation also happens to be the identity sin²x + cos²x  = 1. When you see an expression that can be simplified, using these known identities make working with the equation easier.

Examples of Identities

Other things to take note of to make proving identities easier like the one above is to
Tip 1: Multiply the fraction by the conjugate (opposite signs) of an expression.
Tip 2: Factor
Tip 3: Rewrite the expression in terms of sine and cosine.

Tip 2

Tip1

Tip 3

Graphing Sine Functions

Hi guys! In class we are currently learning how to graph in our circular functions unit. I will be talking about how to graph sine functions. When graphing on a Cartesian plane it is known as “unrolling” the Unit Circle.

The general form for sine is:

y = a sin b(x – c) + d

In order to graph a sine or cosine function you must determine the period and amplitude.

PERIOD is the length of one cycle that can either be in degrees or radians. The period for sinx or cosx functions can be found with the formula  2π / |b| 


AMPLITUDE  is the distance from the middle axis to the highest or lowest point for a sinx or cosx function. Amplitude can be found by taking the absolute value of "a"  

Amplitude = |a|    or    Amplitude = max-min / 2

Now that you have a better understanding of what period and amplitude is lets try an example: 

Sketch the graph of y = 2sin2x for 0 ≤ x ≤ π

1. First find the period by using the formula 2π / |b|

     

       This means the length for one full cycle of y = 2sin2x is π

2. Now lets find the amplitude by taking the absolute value of "a"

3. You are now ready to graph the sine function! On a graph plot the period on the x-axis and the amplitude on the y-axis. 

  We split the period into 4 sections because of the 4 quadrants in the unit circle (remember we are "unrolling" the Unit Circle).

4. Since we are graphing a sine function plot your points starting from (0, 0). When graphing a cosine function you will start from (0, a). The given equation is positive therefore the next point will be in the positive side at (π/4, 2) The graph should look like a wave.

* Make sure to check for restrictions* 

In this example the restrictions are 0 ≤ x ≤ π since our graph fits the restrictions it is complete! 

I hope my example did not confuse you but instead helped you better understand how to graph a sine 

function. Thank you for reading! 

Trigonometric Equations

what's up everyone

          

           In class, we discussed about unit circles, and special triangles. Right now I wanted to show how can you find the theta in trigonometric equation if there's an interval that is given.

NOTE: SINθ,COSθ,TANθ can be X 

Steps to solve for theta  "θ"

• Simplify by isolating the trigonometric ratio or factoring
• Determine the reference angle 
• Cast rule is very important!!!!!!!!!!!!!!!!!!!!!!!!!!!!
• Check the interval given
• State values for "θ" in degrees or radian

Example: solve for "θ" over the indicated interval.

a) 2sin²θ=3sinθ-1, interval 0 <(or equal) θ <(or equal) 2(pi)---------->

-Plug in x for sine to understand the equation------->

-The sine theta equals 1/2 is positive on quadrant 1 and 2

-Sine theta equals 1 is quadrantal angle which is π/2

-The theta R is π/6

-π/6 is from quadrant 1 and 5π/6 is from quadrant 2

Special Right Traingles

Hello! The topic that I'm going to talk about is important because this helps us get some points in the unit circle. They are called the Special Right Angled Triangles.

The angles in this triangles includes 30˚, 45˚ and 60˚ and in radians it's π/6, π/4 and π/3 respectively

But first we have to learn the Six Trigonometric Functions 

•         Sin θ= O/H
•         Cos θ= A/H
•         Tan θ= O/A
•         Csc θ= H/O
•         Sec θ=H/A
•         Cot θ= A/O

   First is the 45˚  triangle using an isosceles triangle. For us to find the sides of this triangle, we assume that the value of the adjacent and the opposite sides are 1. and to compute for the hypotenuse we use the Pythagoras' Theorem. 

    Next is for the 30˚ special triangle. Its adjacent side is calculated with also using the Pythagoras' Theorem. The opposite side is 1 and the hypotenuse is 2.    
    

    Last is the 60˚ special triangle. The value of its sides are the same with the 30˚ triangle. It's just that the opposite side is the square root of 3 and the adjacent side is 1. The hypostenuse stays the same with 2.

j

   

Introduction to Circular Functions

Hey Guys!

Today's class reviewed some trigonometric topics covered in Grade 11 Pre-Cal, as well as introduced Radians and examined the relationship between the value of π and angles both in Degrees and Radians. The discovery of this relationship allowed us to calculate either Radians or Degrees.

Reviewed Grade 11 topics:

TERMINOLOGY:

- Initial Side = The position at which the ray originates

- Terminal Side = The position at which the ray ends/terminates

- Reference Angle = The angle between the terminal arm and the x-axis. This value is less than 90°  
                             


OTHER:

- An unknown Angular measurement is denoted by the Greet letter theta

New Concepts: 

- Radians = A unit of angular measurement 

                   Important Note: The value of the central angle that intercepts the arc is 1 Radian when the arc of a circle is  
                                                     equal to the radius of the circle.

                                                     EQUATION:   Central angle = arc length
                                                                              1 Rotation       circumference 


- π is the approximate Radian value of 3.141592654, and correlates with the Degree value of 180°.

π = 180° = 3.141592654

- Converting between Degrees and Radians 

- Recognizing the Relationship between Pi and Degree measurements

If π = 180° then 2π = 360°
If π = 180° then π/2 = 90°
If π = 180° then 3π/2 = 270°

We can then apply the relationship between π and Degrees to Graph labelling

- In addition, we examined the correlation between the number of revolutions made and the Degree measurement, allowing us to further calculate Radians in both exact and approximate values.

- Direction of Rotation 
 
Positive = Counter-Clockwise
Negative = Clockwise

•    Counter-Clockwise rotation is denoted by a positive angular measurement

              ex.) 90° = rotation of 90° in a counter-clockwise direction of rotation
                                                        or
                     1.57 = rotation of 1.57 Radians in a counter-clockwise direction of rotation

•    Clockwise rotation is denoted by a negative angular measurement

              ex.) -90° = rotation of 90° in a clockwise direction of rotation
                                                    or
                    -1.57 = rotation of 1.57 Radians in a clockwise direction of rotation

- Co-Terminal Angles

 - These are angles which share terminal sides

Rational Root Theorem

Hi Pre-Calculus friends! So from the previous blog post, Lea talked about how to divide using long and synthetic division. She mentioned that P(a)=Remainder and that if the remainder equals to 0, it is a factor of the polynomial. These information and methods are important to know when you are trying to find possible roots of a polynomial.

When you are given a polynomial, there is an "a" and "k" which are labelled below. 

Finding the factors of k and a and dividing them will help you look for a remainder of zero(a factor)

Let's try an example:

Example 1: Write the factors that can be tried in the polynomial to check for rational roots of P(x), given, 

Now let's try to do an example on how to find possible roots by doing it step by step.

Example 2: Find the possible roots of: 

I hope my examples and steps will help you find real roots of a polynomial function. It will be the same steps with any other polynomial function.

Halloween 2015

Long and Synthetic Division

Hi there! Let's review the first part that we've covered in Unit 3 so far. In this unit, we mostly use division to find the answers, which could be either Long Division or Synthetic Division. However, there are certain points that we have to remember when use these methods.


Example 1: Divide 16t + 6t³ - 4- 19x²  by t -2

Long division                                                                     

-Always arrange the terms from                                      

highest to lowest degree

-Use subtraction                                                               

                                                                                             

OR WE CAN USE,

Synthetic Division

 -The arrangement of the coefficients is based from

 highest to lowest degree

 -Use Addition

-The divisor will be 2 because (x-a) → t-2 → x=2

• 6t³ -19t² +16t -4 ÷  t -2 =  6t² -7t +2
• Factor the quotient 6t² -7t +2 

       6t² -7t +2                                                            

       6t² -4t -3t +2

       2t (3t-2) -1 (3t -2)

       (2t -1) (3t-2)

Answer:  6t³ -19t² +16t -4 =  (2t -1) (3t-2) (t -2)

A remainder of 0 means the divisor is a factor of the given polynomial

Example 2: Divide x -2 +4x² +x³ by x -1

Long Division                                                                                        

-Arrange the terms from                                                                    

highest to lowest degree again                                                         

-Use subtraction

OR WE CAN USE,

 Synthetic Division

 -The arrangement of the coefficients is based from

 highest to lowest

  -Use Addition

-The divisor will be -3 because (x-a) → t+3 → x= -3

x³ +4x² +x -2 ÷  x -1 =  x² +5x +6

Factor the quotient x² +5x +6

x² +5x +6

x² +3x +2x +6

x(x+3) 2(x+3)

(x+2) (x+3)

A remainder of more than 0 means the divisor is not a factor of the given polynomial

To conclude, it's way easier to use synthetic division but try doing long division once in a while since it's a good practice. 

Going Backwards with Transformations

       A couple of days ago, we learned how to graph y= f(x) if the transformed function is given. We can determine the original function y=f(x) when the transformed function is given, by first determining what transformation(s) occurred in the function. Then, reverses the steps of transformation(s) after doing so, apply the opposite operation to the x and y point(s).

Example:

-        Given the transformed function y= 2f ½ (x+2) -1 below. What is the graph of y= f(x).

       Transformation:             To get y= f(x)                        

     - Multiply y-values by 2            - Add 1 from y-values

     - Subtract 1 from y-values         - Divide y-values by 2

     - Multiply x-values by 2           - Add 2 from x-values

     - Subtract 2 from x-values        - Divide x-values by 2

                        

     

                                                        y= 2f ½ (x+2) -1        y= f(x)

                                          (-1, 1)                      (½, 3/2)

                                                          (2, -2)                      (5/2, ­­-½)

                                                          (4,-2)                       (4, -½)

                                                          (6, 0)                       (5, ½)